Time measurement with astronomical phenomena (Earth rotation on itself or around the sun, pulsars) is based on the link between the flow of time and the linear evolution of a parameter, usually a rotation angle. This principle is identical to that of the hourglass or the clepsydra which associates a duration measurement with the variation – as linear as possible – of a sand or liquid height thus visualizing the time “flow”. The advantage of this measurement type is providing a direct time or duration reference, which placed these astronomical measurements at the heart of the definition of the second in the International System of Units until 1967, year of the new definition of the second based on a periodic quantum system put into practice in atomic clocks. Precision of atomic clocks allows us today to measure very precisely the Earth’s rotation speed fluctuations due to geophysical, hydrological and atmospheric phenomena.

Duration measurement with a periodic system consists simply in counting the number of periods contained in this duration. The oscillator then plays the role of a “time ruler”, by analogy with length measurement obtained by counting a ruler’s graduations. We can deduce from this simple description a very important rule which still underlies today all the oscillators and atomic clocks developments in the race for accuracy: duration measurement precision is all the greater as the number of periods counted is large, i.e., the “temporal graduation” is fine, or even that the oscillator frequency is high.

This rule has resulted in a considerable increase in the oscillators frequency, from mechanical oscillators vibrating at a few hertz to optical oscillators (lasers) emitting signals at several hundred terahertz (1 THz =10¹² Hz) and used in current optical clocks.

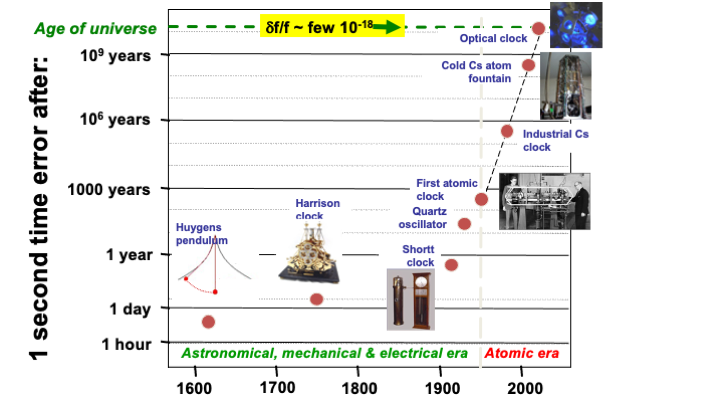
From Galileo’s invention of the pendulum at the beginning of the 17th century to today’s atomic clocks, time measurement with periodic phenomena has experienced a tremendous development, with an improvement in accuracy of sixteen orders of magnitude over four centuries. Thus, the best current optical clocks have a frequency uncertainty of some 10^-18, which would correspond to an error of the order of a second in the age of the universe.